以前紹介した 室内測位システム ではフレームの姿勢をMAVLinkで貰ってるんですが室内なのとコアレスモーターがついてるせいでフレームに載せているコンパスがくるってしまい、それで得られるyawの値も酷いものなので代わりに天井のカムからみたマーカーで推定できるヘッドの方向を使っています.

一般には斜め上からみることになるので頭と尾のマーカーがちょうど南北を向いているように見えても機体が水平でないと実際には南北を向いていません. 絵で書くとこんな感じになります

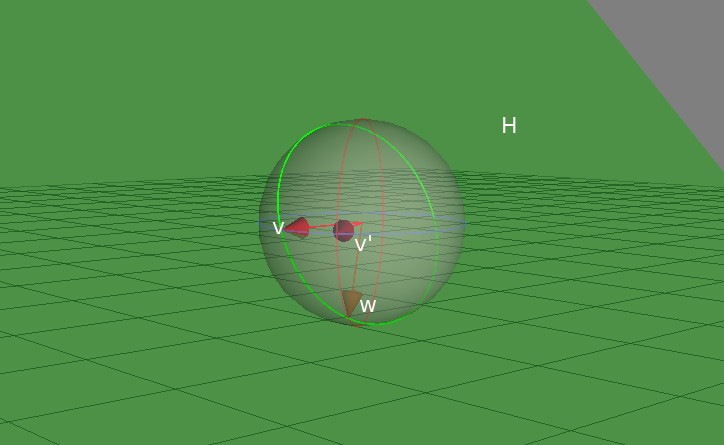
wが機体の頭と尾のマーカーを結んだ直線の方向でカムからこれをみると方向がvであるかのように見えています. 実際は真上から見た方向v'をpitchの分だけ回転したのがwなわけです. 斜めになった緑の面Hはカムやvやwを含む平面です.

なので問題は見かけの方向を機首の上げ下げの情報で修正する、つまり

vとpitchからwを求める

になります. 通常このような問題は回転行列や球面角で計算するのだと思うのですがgeometric algebraを使って求めることができます.

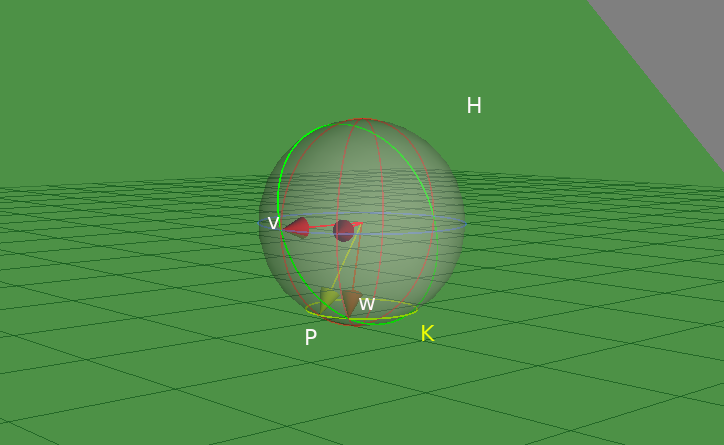
図のようにvをvとz-軸方向でできる面内でpitchだけ回転した黄色のベクトルの終点をPとしてこの点を通って水平に球上を回る円周Kを描きます. wの終点はK上にあるはずです. vとwを含む面Hはvとカムから球の中心への方向uとを含む面でもあるのでKとHの2つの交点のどちらかの表す方向がwになります. これらの操作はgeometric algebraでの簡単な操作に対応していてlibvsrだと

auto bi = v ^ Vec(0, 0, 1);
auto rop = Gen::rot(bi*(-pitch_angle/2));
auto H = (PT(0, 0, 0) ^ v ^ u ^ Inf(1)).dual();
auto K = v.sp(rop).null() ^ Biv::xy;
auto pp = H <= K;
auto w = Round::split(pp, true);

というようなプログラムになります.

HとKの交点を求める操作はgeometric algebraではmeetと呼ばれる演算でこの場合の結果は点対(point pair)と呼ばれるものになります. 実はKやHそしてこの点対ppには向きがあり、その向きで点対の2点には順番がつけられます. Round::splitは第二引数がtrueなら最初のそうでなければ2番目の点を返す静的メソッドです. 上のプログラムでは向きまで考えると点対の最初の点がwになります.

結果をyaw角に直したければ

yaw_meas = atan2f(w[1], w[0]);

とすればokです. 回転行列や球面角を使うと中間計算で三角関数を多用することになりライブラリなどを使うとしてもいろいろとめんどうなのですが、geometric algebraでは描いた絵をほぼそのままプログラムにしてしまえることがわかると思います.

得られたyaw角は当然カムでの測定時の誤差などいろいろなノイズがのっているのでそのままではなくカルマンフィルターを使ってその推定値を利用しています. そもそもそれ程の精度はないのですがそれでもコンパスで得られるyawの値よりだいぶまともなようです. この測位系での ホバーリング もだいぶ安定したものになりました.