Conformal model of 3D space

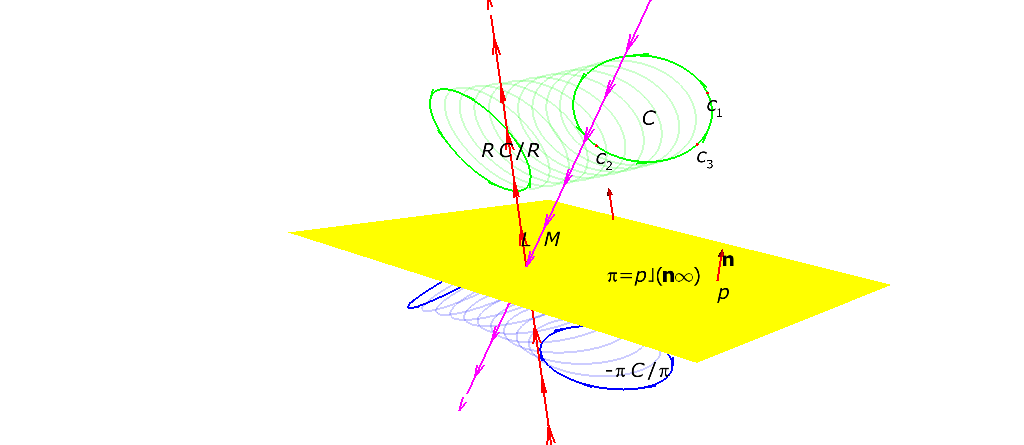(Fig.1.1 of the book)

The conformal model is an ample model of the 3D space. Points, lines, planes, circles, spheres and many known geometrical constructions can be represented with algebraic ways in that model.

There are 2 additional bases of this representation space. One is o which represents "origin" and the other one is ∞ which means "infinity". For readability, write "no" for o and "ni" for ∞. The 3D point (x, y, z) can be represented as the 5D point no + x e1 + y e2 + z e3 + 0.5 α ni where α = x x + y y + z z and e1-3 are "euclidean" bases.

It looks very strange and somewhat artificial but turns out to be a surprisingly fine embedding. It's also a good extension of homogeneous model. In this world, we have the unit "psudoscalar" I = no^e1^e2^e3^ni which behaves like a "complete" element where ^ is the outer(wedge) product. With it, a bit unpopular construction "dual" of A can be defined to be A/I and denoded by A*.

When p,q,r,s are 4 3D points with a general position represented in this model space, S = p^q^r^s represents a sphere on which those 4 points are. It's known that S* = c - 0.5 rho rho ni where c is the center of S and rho is the radius of S. Looks things go well, don't they?

Rotation, translation and another "conformal" transformation can be described with the uniform manner -- "versor" in this model. They give not only theoritical but also computational tools in the real applications. I hear that the Unreal Engin uses the conformal model and the geometric algebra in their lighting computations.

Plunge

There are intresting constructions which are a bit unpopular. "Plunge" is one of them. An example of plunge is here.

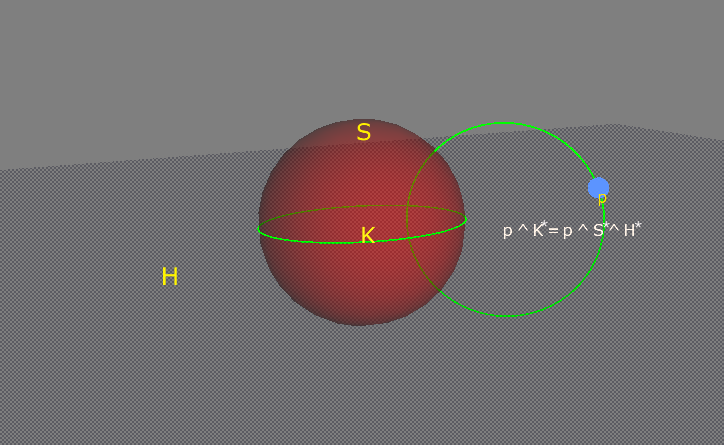
The circle labeled p ^ K* is the plunge of p, S and H. It crosses perpendicularly to the point p, the sphere S and the plane H.

A circle of latitude can be considered as another example of plunge.

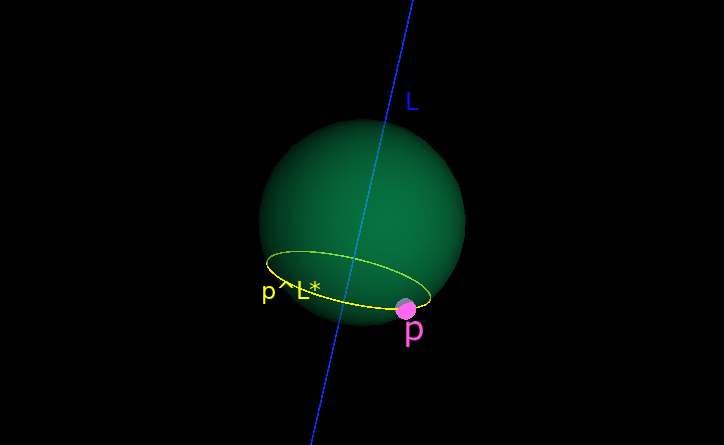
If you live in point p on this sphere surface not poles, then p ^ L* is the circle of latitude passes p where L is the earth's axis. Since L can be a meet of two planes H and H', p ^ L* = p ^ H* ^ H'* which is the plunge of p, H and H'.

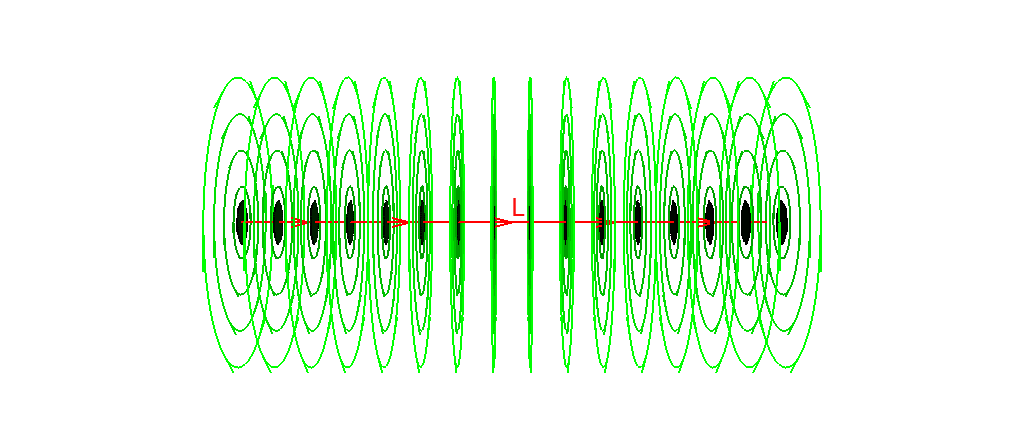
This is Fig.15.5 of the book which shows many circles p ^ L* for various points p. Now L* looks like the field of possible circles, doesn't it?